سیستم عددی باینری یکی از چهار نوع سیستم عددی است. در برنامه‌های کامپیوتری، که در آن‌ها اعداد باینری تنها با دو نماد یا رقم نمایش داده می‌شوند، یعنی ۰ (صفر) و ۱ (یک)، اعداد باینری در اینجا در سیستم عددی مبنای ۲ بیان می‌شوند. به عنوان مثال، 2(101)یک عدد باینری است. هر رقم در این سیستم به آن "بیت" گفته می‌شود. برای آشنایی بیشتر با سیستم‌های عددی، اینجا را مطالعه کنید.
سیستم عددی روشی برای نمایش اعداد در معماری کامپیوتر است. چهار نوع مختلف از سیستم عددی وجود دارد، مانند:
سیستم عددی باینری (مبنای ۲)
سیستم عددی هشت‌گانه (مبنای ۸)
سیستم عددی ده‌دهی (مبنای ۱۰)
سیستم عددی شانزده‌گانه (مبنای ۱۶)
در این مقاله، در مورد سیستم عددی باینری، تبدیل از یک سیستم به سیستم‌های دیگر، جدول‌ها، موقعیت‌ها، عملیات‌های باینری مانند جمع، تفریق، ضرب و تقسیم، کاربردها و مثال‌های حل‌شده به طور مفصل صحبت می کنیم.
سیستم عددی باینری(Binary) چیست؟
سیستم عددی باینری: طبق اصول الکترونیک دیجیتال و ریاضیات، عدد باینری به عددی گفته می‌شود که در سیستم عددی باینری یا سیستم عددی مبنای ۲ بیان می‌شود. این سیستم مقادیر عددی را با دو نماد جداگانه بیان می‌کند؛ ۱ (یک) و ۰ (صفر). سیستم مبنای ۲ یک نمایش موقعیتی است که در آن ۲ به عنوان رادیکس (پایه) استفاده می‌شود.
سیستم باینری به طور داخلی توسط تقریباً تمام کامپیوترهای جدید و دستگاه‌های مبتنی بر کامپیوتر استفاده می‌شود، زیرا به راحتی در مدارهای الکترونیکی با استفاده از دروازه‌های منطقی پیاده‌سازی می‌شود. هر رقم در این سیستم به عنوان "بیت" شناخته می‌شود.
مثال: تبدیل عدد ۴ به باینری.
راه‌حل:
۴ به باینری معادل 2(100) است.
در اینجا، ۴ در سیستم عددی ده‌دهی نمایش داده شده است، جایی که می‌توانیم عدد را با استفاده از ارقام ۰ تا ۹ نمایش دهیم. اما در سیستم عددی باینری، فقط از دو رقم ۰ و ۱ استفاده می‌کنیم.
حالا، بیایید در مورد نحوه تبدیل ۴ به سیستم عددی باینری صحبت کنیم. مراحل زیر برای تبدیل ۴ به باینری کمک می‌کند.
گام ۱: ابتدا عدد ۴ را بر ۲ تقسیم کنید. حاصل‌ضرب صحیح به دست آمده در این گام را به عنوان مقسوم علیه برای گام بعدی استفاده کنید. این گام را ادامه دهید تا زمانی که حاصل‌ضرب برابر ۰ شود.
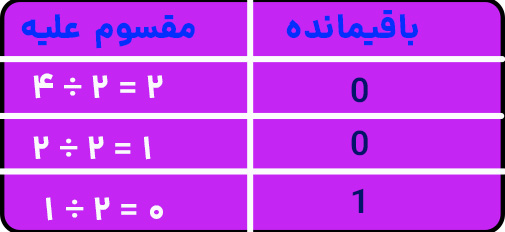
گام ۲: حالا، باقی‌مانده‌ها را به ترتیب معکوس زمانی بنویسید. (یعنی از پایین به بالا).
در اینجا، کم‌ترین بیت قابل توجه (LSB) برابر ۰ و بزرگ‌ترین بیت قابل توجه (MSB) برابر ۱ است.
بنابراین، عدد ۴ در سیستم باینری معادل ۱۰۰₂ است.
پس، اگر بخواهیم تعداد بیت‌های عدد ۴ در سیستم باینری را پیدا کنیم، باید تعداد صفرها و یک‌ها را بشماریم.
پس، ۴ در سیستم باینری معادل ۱۰۰₂ است. در اینجا، ۲ عدد صفر و ۱ عدد یک داریم. بنابراین، تعداد بیت‌ها ۳ عدد است.
بنابراین، تعداد بیت‌های عدد ۴ در سیستم باینری برابر ۳ است.
بیت در سیستم عددی باینری چیست؟
یک رقم واحد باینری "بیت" نامیده می‌شود. یک عدد باینری از چندین بیت تشکیل شده است. مثال‌ها عبارتند از:
۱۰۱۰۱ یک عدد باینری پنج‌بیتی است
۱۰۱ یک عدد باینری سه‌بیتی است
۱۰۰۰۰۱ یک عدد باینری شش‌بیتی است
نکات قابل توجه:
اعداد باینری تنها از ۰ و ۱ ساخته شده‌اند.
یک عدد باینری با مبنای ۲ نمایش داده می‌شود.
یک بیت یک رقم واحد باینری است.
جدول اعداد دودویی
برخی از نمادهای دودویی برای فهرستی از اعداد ده‌دهی از ۱ تا ۳۰ در لیست زیر ذکر شده است.
| عدد | عدد دودویی | عدد | عدد دودویی | عدد | عدد دودویی |
|---|---|---|---|---|---|
| 1 | 1 | 11 | 1011 | 21 | 10101 |
| 2 | 10 | 12 | 1100 | 22 | 10110 |
| 3 | 11 | 13 | 1101 | 23 | 10111 |
| 4 | 100 | 14 | 1110 | 24 | 11000 |
| 5 | 101 | 15 | 1111 | 25 | 11001 |
| 6 | 110 | 16 | 10000 | 26 | 11010 |
| 7 | 111 | 17 | 10001 | 27 | 11011 |
| 8 | 1000 | 18 | 10010 | 28 | 11100 |
| 9 | 1001 | 19 | 10011 | 29 | 11101 |
| 10 | 1010 | 20 | 10100 | 30 | 11110 |
چگونه اعداد دودویی را محاسبه کنیم؟
برای مثال، عددی که باید عملیات روی آن انجام شود، ۱۲۳۵ است.
| هزارگان | صدگان | دهگان | یکان |
|---|---|---|---|
| 5 | 3 | 2 | 1 |
این نشان می‌دهد که:
۱ × ۱۰۰۰ + ۲ × ۱۰۰ + ۳ × ۱۰ + ۵ × ۱=1235
با توجه به اینکه:
103 = 10 × 10 × 10 = | 1000 |
10×10= 102= | 100 |
10= 10¹ = | 10 |
(هر عدد به توان صفر برابر با یک است) 100 | 1 |
جدول بالا را می‌توان به این صورت توصیف کرد:
| هزارگان | صدگان | دهگان | یکان |
|---|---|---|---|
| ۱۰³ | ۱۰² | ۱۰¹ | ۱۰⁰ |
| ۱ | ۲ | ۳ | ۵ |
بنابراین:
1235 = 1 × 1000 + 2 × 100 + 3 × 10 + 5 × 1
= 1 × 103 + 2 × 102 + 3 × 101 + 5 × 100
مقایسه سیستم دودویی و ده‌دهی
از آنجا که سیستم دودویی تنها از دو رقم یا بیت استفاده می‌کند و اعداد را با الگوهای مختلفی از ۱ و ۰ نمایش می‌دهد، به عنوان یک سیستم مبنای ۲ شناخته می‌شود. در این سیستم:
- ۱ نشان‌دهنده حالت روشن یا درست است.
- ۰ نشان‌دهنده حالت خاموش یا نادرست است.
در مقابل، سیستم ده‌دهی یک سیستم مبنای ۱۰ است که در آن هر جایگاه عدد می‌تواند یکی از ۱۰ رقم ممکن (۰ تا ۹) را داشته باشد.
در یک عدد چندرقمی:
- سمت راست‌ترین رقم در مرتبه یکان قرار دارد.
- رقم بعدی در سمت چپ، در مرتبه دهگان قرار می‌گیرد.
- رقم بعد از آن در سمت چپ، در مرتبه صدگان قرار دارد و این روند ادامه پیدا می‌کند.
اهمیت کد دودویی
سیستم عددی دودویی پایه و اساس تمام سیستم‌ها و عملیات‌های محاسباتی است. این سیستم به دستگاه‌ها امکان می‌دهد تا انواع مختلف اطلاعات را که به پردازنده (CPU) یا حافظه ارسال و دریافت می‌شود، ذخیره، دسترسی و پردازش کنند. این قابلیت، توسعه برنامه‌هایی را ممکن می‌سازد که کاربران بتوانند:
- وب‌سایت‌ها را مشاهده کنند؛
- اسناد را ایجاد و به‌روزرسانی کنند؛
- بازی کنند؛
- ویدئوهای استریم و انواع دیگر اطلاعات گرافیکی را مشاهده کنند؛
- به نرم‌افزارها دسترسی داشته باشند؛
- و محاسبات و تحلیل داده‌ها را انجام دهند.
طرح دودویی دیجیتالی که شامل ۱ها و ۰ها است، روشی ساده و زیبا برای کارکرد کامپیوترها فراهم می‌کند. این روش همچنین راهی کارآمد برای کنترل مدارهای منطقی و تشخیص وضعیت درست (۱) و نادرست (۰) سیگنال‌های الکتریکی ارائه می‌دهد.
برای افزودن دیدگاه خود، نیاز است ابتدا وارد حساب کاربری‌تان شوید